GameObject 의 Scale, Rotation, Translation 을 처리할 컴포넌트를 생성해서 코드를 모듈화 해본다. Component 클래스를 만들고, 이 클래스를 상속받아 Transform 컴포넌트를 생성해줌. 유니티의 그것과 동일한 네이밍. 동일한 기능을 만들어본다.
Transform 클래스를 만들고, GameObject 가 들고있던 _localScale, _localRotation, _localPosition 을 옮겨줌. 관련 Get/Set 메소드들도 모두 만들어준다. 로컬좌표계의 SRT 변환을 처리해줄 행렬 Matrix _matLocal 을 생성해주고, 이 행렬을 활용해서 월드좌표를 계산할 메소드 UpdateTransform() 함수를 만들어준다.
#include "Component.h"class Transform : public Component
{
using Super = Component;
public:
Transform() {}
virtual ~Transform() {}
virtual void Init() override;
virtual void Update() override;
void UpdateTransform();
Vec3 GetLocalScale() { return _localScale; }
void SetLocalScale(const Vec3& localScale) { _localScale = localScale; }
Vec3 GetLocalRotation() { return _localRotation; }
void SetLocalRotation(const Vec3& localRotation) { _localRotation = localRotation; }
Vec3 GetLocalPosition() { return _localPosition; }
void SetLocalPosition(const Vec3& localPosition) { _localPosition = localPosition; }
// World SRT 벡터 관련 메소드를 만들어야 함.
private:
Vec3 _localScale = { 1.f, 1.f, 1.f };
Vec3 _localRotation = { 0.f, 0.f, 0.f };
Vec3 _localPosition = { 0.f, 0.f, 0.f };
// 로컬 SRT 변환 행렬.
Matrix _matLocal = Matrix::Identity;
Matrix _matWorld = Matrix::Identity;
Vec3 _scale;
Vec3 _rotation;
Vec3 _position;
Vec3 _right;
Vec3 _up;
Vec3 _look;
};이 GameObject, Transform 에서 월드좌표를 구하려면 부모의 Transform 을 참조해야 함. 부모의 SRT 를 알아와서 곱해야 월드좌표를 알 수 있기 때문에.
shared_ptr<Transform> _parent; // 부모
vector<shared_ptr<Transform>> _children; // 자식들UpdateTransform() 함수는 GameObject 하위의 Update() 함수 내용을 옮긴 뒤 World Transform 이 적용되도록 적절히 수정. 만약 이 Transform 이 항상 월드에 있다면, _matWorld = _matLocal 이 됨. 만약 부모 Transform 이 존재한다면 부모의 WorldMatrix를 곱해주는 추가 연산이 필요.
void Transform::UpdateTransform()
{
Matrix matScale = Matrix::CreateScale(_localScale);
Matrix matRotation = Matrix::CreateRotationX(_localRotation.x);
matRotation *= Matrix::CreateRotationY(_localRotation.y);
matRotation *= Matrix::CreateRotationZ(_localRotation.z);
Matrix matTranslation = Matrix::CreateTranslation(_localPosition);
_matLocal = matScale * matRotation * matTranslation; // SRT
if (!HasParent())
{
_matWorld = _matLocal;
}
else
{
_matWorld = _matLocal * _parent->GetWorldMatrix();
}
}다음은 현재 Transform 의 Scale, Rotion, Translation 벡터를 각각 Local Matrix 로부터 구해보기. SimpleMath의 Matrix::Decompose() 함수로 구할 수 있는데, Rotation은 Euler 형식의 벡터가 아닌 Quaternion 사원수로만 받을 수 있음. 사원수 Quaternion 은 struct Quaternion : public XMFLOAT4 타입.
Quaternion 으로 받은 Rotation 은 인터넷 검색으로 Euler 각으로 변환하는 함수를 통해 Vec3 Rotation 으로 변환. 아래 QuaternionToEulerAngles 함수는 아래에서 긁어옴.
// https://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles
{
//...
Quaternion quaternion;
_matWorld.Decompose(_scale, quaternion, _position); // SRT 요소 획득.
// Quaternion 을 Euler 로 변환
_rotation = QuaternionToEulerAngles(quaternion);
}
Vec3 QuaternionToEulerAngles(Quaternion q) {
const double M_PI = 3.14159f;
Vec3 retAngles;
// roll (x-axis rotation)
double sinr_cosp = 2 * (q.w * q.x + q.y * q.z);
double cosr_cosp = 1 - 2 * (q.x * q.x + q.y * q.y);
retAngles.x = std::atan2(sinr_cosp, cosr_cosp);
// pitch (y-axis rotation)
double sinp = std::sqrt(1 + 2 * (q.w * q.y - q.x * q.z));
double cosp = std::sqrt(1 - 2 * (q.w * q.y - q.x * q.z));
retAngles.y = 2 * std::atan2(sinp, cosp) - M_PI / 2;
// yaw (z-axis rotation)
double siny_cosp = 2 * (q.w * q.z + q.x * q.y);
double cosy_cosp = 1 - 2 * (q.y * q.y + q.z * q.z);
retAngles.z = std::atan2(siny_cosp, cosy_cosp);
return retAngles;
}
다음은 right, up, look 벡터를 구해준다.
유의해야할 점은. SimpleMath::Vector3::Transform 함수. 위치값 적용은 필요 없으니 TransformNormal 을 사용하면 되고,
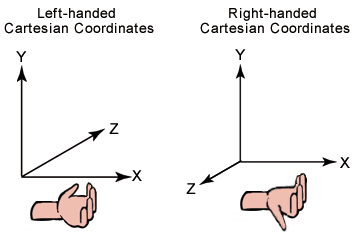
_look 벡터를 구할 때, SimpleMath 가 오른손 좌표계 기준이기 때문에 Forward 가 0,0,-1 이라서 _look 벡터는 Backward 를 기준으로 구해줘야 함.

_right = Vec3::TransformNormal(Vec3::Right, _matWorld);
_up = Vec3::TransformNormal(Vec3::Up, _matWorld);
_look = Vec3::TransformNormal(Vec3::Backward, _matWorld);마지막으로 자식 Transform 들도 모두 업데이트 호출.
for (const shared_ptr<Transform>& child : _children)
{
child->UpdateTransform();
}이렇게 작성한 UpdateTransform() 함수는 Transform 이 변경될 때마다 한 번씩 호출해줘서 부모 자식간의 계층구조에 필요한 값들을 모두 갱신 처리 해줘야 함.
이제 Transform 에서 world의 Scale, Roation, Position을 Get/Set 하는 메소드가 필요. Get 메소드들은 위에서 구한 _scale, _rotation, _position 을 그냥 뱉어주면 되는데 Set~ 메소드들은 내부에서 부모와의 관계를 고려해서 처리 해줘야 함.
Vec3 GetScale() { return _scale; }
void SetScale(const Vec3& scale);
Vec3 GetRotation() { return _rotation; }
void SetRotation(const Vec3& rotation);
Vec3 GetPosition() { return _position; }
void SetPosition(const Vec3& position);SetScale, SetRotation, SetPosition 은 parent 가 있을 경우 parent 의 Scale 값이나 Matrix 의 역을 취해서 연산을 해줘야 함.
void Transform::SetScale(const Vec3& worldScale)
{
if (HasParent())
{
Vec3 parentScale = _parent->GetScale();
Vec3 scale = worldScale;
scale.x /= parentScale.x;
scale.y /= parentScale.y;
scale.z /= parentScale.z;
SetLocalScale(scale);
}
else
{
SetLocalScale(worldScale);
}
}
void Transform::SetRotation(const Vec3& worldRotation)
{
if (HasParent())
{
Matrix matParentInverse = _parent->GetWorldMatrix().Invert();
Vec3 rotation;
rotation = Vec3::TransformNormal(worldRotation, matParentInverse);
SetLocalRotation(rotation);
}
else
{
SetLocalRotation(worldRotation);
}
}
void Transform::SetPosition(const Vec3& worldPosition)
{
if (HasParent())
{
Matrix matParentInverse = _parent->GetWorldMatrix().Invert();
Vec3 position;
position = Vec3::Transform(worldPosition, matParentInverse);
SetLocalPosition(position);
}
else
{
SetLocalPosition(worldPosition);
}
}Transform 컴포넌트는 여기까지.
<리얼-타임 렌더링(REAL-TIME RENDERING) 4/e> 구입 링크
https://link.coupang.com/a/8VWas
리얼-타임 렌더링 4/e
COUPANG
www.coupang.com
<DirectX 12를 이용한 3D 게임 프로그래밍 입문> 구입 링크
https://link.coupang.com/a/8V4Wq
DirectX 12를 이용한 3D 게임 프로그래밍 입문:게임 개발 중심으로 익히는 대화식 컴퓨터 그래픽 프
COUPANG
www.coupang.com
<이득우의 게임 수학:39가지 예제로 배운다! 메타버스를 구성하는 게임 수학의 모든 것> 구입 링크
https://link.coupang.com/a/9BqLd
이득우의 게임 수학:39가지 예제로 배운다! 메타버스를 구성하는 게임 수학의 모든 것
COUPANG
www.coupang.com
유니티 에셋 스토어 링크
https://assetstore.unity.com?aid=1011lvz7h
에셋스토어
여러분의 작업에 필요한 베스트 에셋을 찾아보세요. 유니티 에셋스토어가 2D, 3D 모델, SDK, 템플릿, 툴 등 여러분의 콘텐츠 제작에 날개를 달아줄 다양한 에셋을 제공합니다.
assetstore.unity.com
(링크를 통해 도서/에셋 구입시 일정액의 수수료를 지급받습니다.)
'게임 개발 자료 > DirectX 스터디' 카테고리의 다른 글
| DirectX 11 스터디 관련 글 스크랩 및 메모 (0) | 2023.09.27 |
|---|---|
| DirectX 11 스터디 - MeshRenderer 컴포넌트 (GameObject 완) (0) | 2023.09.26 |
| DirectX 11 스터디 - Camera 컴포넌트 (0) | 2023.09.26 |
| DirectX 11 스터디 - 고유 물체를 정의할 GameObject 만들기 (0) | 2023.09.20 |
| DirectX 11 스터디 - 모듈화 (2), 렌더링을 책임질 Pipeline클래스 작성 (0) | 2023.09.20 |
| DirectX 11 스터디 - 모듈화 (1) (0) | 2023.09.19 |
| 행렬(Matrix) 스터디 - 실습 및 SimpleMath for DirectXMath (0) | 2023.09.14 |